Challenge 7 – Exploring the Lunar Shadow Conet
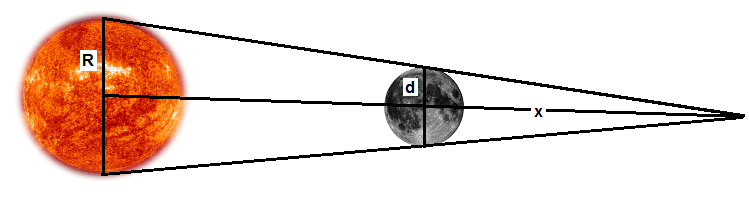
Any object in our solar system casts a shadow behind it as the sun’s rays of light are blocked by the object. The length of this ‘shadow cone’ depends on the diameter of the object and its distance from the sun.
Lunar shadow figure
Credit: Sten Odenwald NASA HEC
Problem 1 – At the time of the August 21, 23017 total solar eclipse, the distance from the center of Earth to the center of the sun is 151,390,000 kilometers, and the center of the moon is located 372,000 kilometers from the center of Earth in the direction of the sun. Using similar triangles, what is X, the length of the lunar shadow cone if the radius of the sun is 696,300 km and the radius of the moon is 1737 km to 4 significant figures?
Now the moon is 372,027 km sunwards of the Earth’s center (USNO), so the vertex of the shadow cone is 377,700 – 372,027 = 5,673 km (to 4-SF) from the center of Earth opposite the sun or 6378-5673 = 705 km below the surface of Earth!
Phobos Transit
Credit: NASA / Curiosity
Problem 2 – The Martian moon Phobos often passes between the sun and Mars, and this event has been photographed by NASA’s Curiosity rover as shown below in a series of images on August 20, 2013. How far does the shadow cone of Phobos extend from this small moon? The diameter of Phobos is 25 km, and it orbits at an average distance of 9,300 km from the center of Mars. The average distance from Mars to the sun is 228 million kilometers.